沖縄では 2015 年と並び観測史上最も早い梅雨明けとなり、本州でも梅雨明けを思わせるような天気が続いています。これから少なくとも 9 月末まで、暑い季節の始まります。
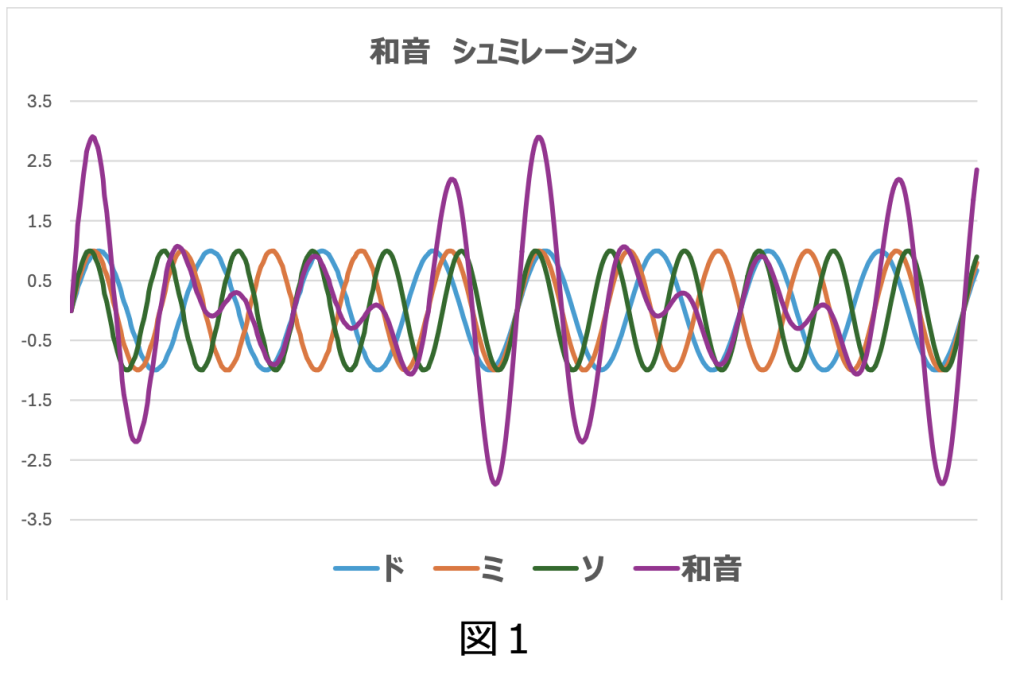
耳による音の検知については前回述べましたが、今回はその詳細です。オーケストラの音や、周囲の環境音は、複数の音源からの音波が重なり合って知覚されるため、その構造は複雑です。今回は音階、具体的には「ドレミファソラシド」の中から、和音である“ドミソ”を例に挙げて単純化して考えてみましょう。和音が美しき聞こえるのは、純正律で“ドミソ”の周波数が 4:5:6 と整数比になるためです。“ファラド”、“ソシレ”も同様です。通常“ド(C4)”と言っている周波数は 261.6Hz で、波⾧に変換すると 1.3m となり、分光の世界で用いる波⾧とは桁違いの⾧さです。
音は空気の振動である音波として伝搬します。“ド”、“ミ”、“ソ”の音波は先に述べたように 4:5:6という単純な整数比を持つ音波の組み合わせになり、簡単にシュミレーションすると図1になります。耳に届く音は様々な音波の和音ですが、その中にどんな音波が含まれるかは、フーリエ変換を用いることにより調べることができます。
下記のようなフーリエ級数の複雑な式をみただけでギブアップです。亀の子=ベンゼン環を見て化学をギブアップした同級生がいましたが、それに近い気分になります。
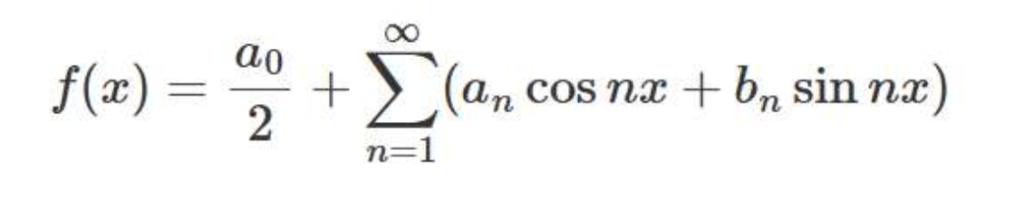
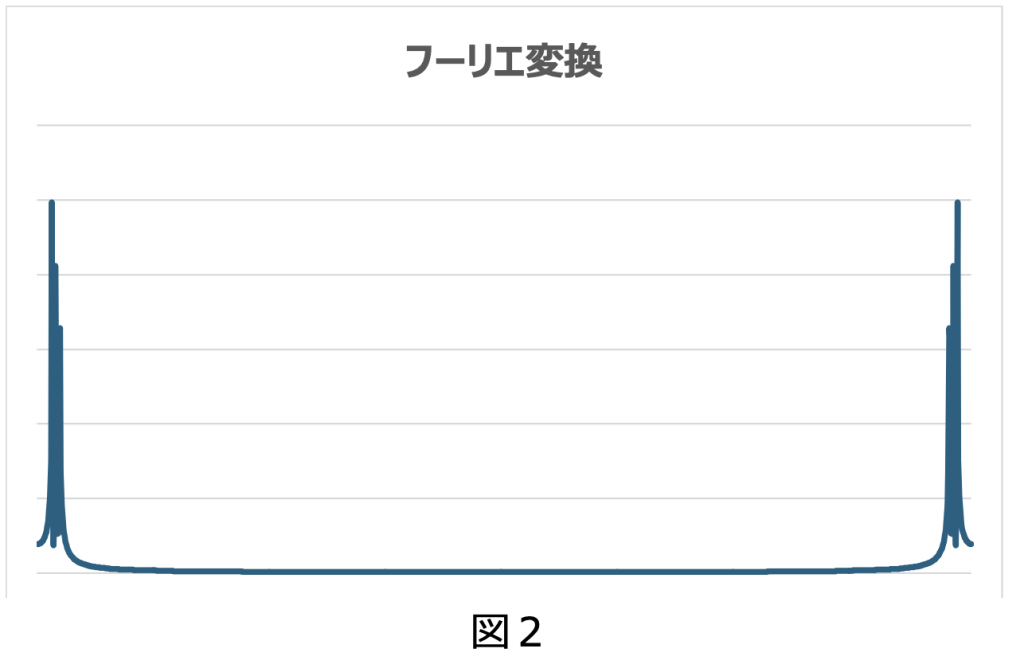
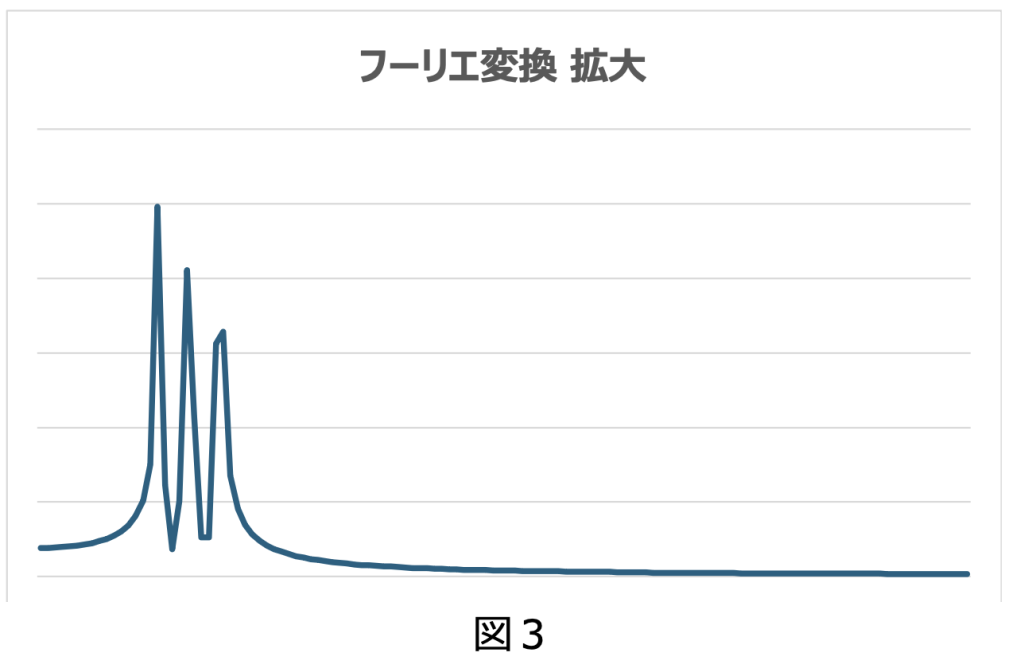
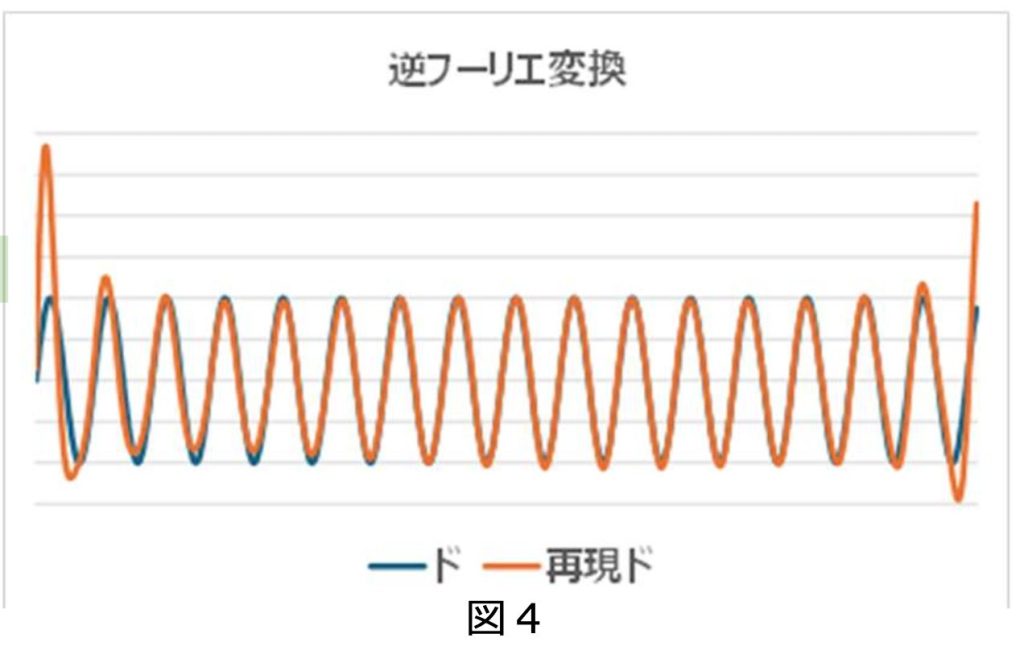
フーリエ変換の結果を逆フーリエ変換すると、理論的に元の音波に戻すことができます。すなわち、“ドミソ”のフーリエ変換結果から“ミ”と“ソ”を除去して逆フーリエ変換を行うと、“ド”の音波が再図4現されます。元の“ド”の音波と、この逆フーリエ変換で再現された音波を重ね合わせた結果が図4です。
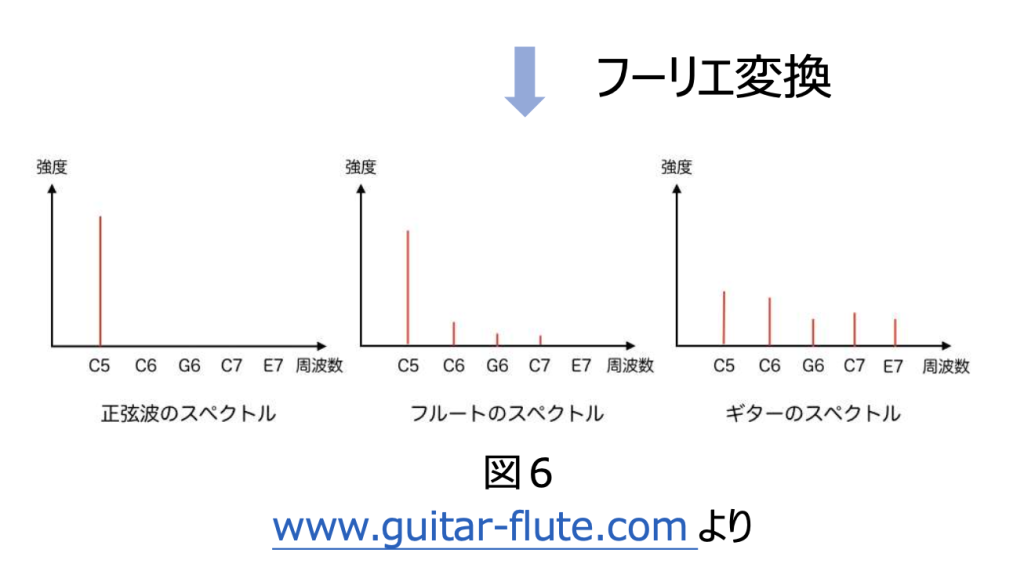
両端に差は見られるものの、ほぼ元の音波が再現されていることがわかります。この例は正弦波をシミュレーションした結果ですが、実際の楽器や人によって、同じ音でも波形が変わります。これの波形の違いが、音色の違いとして耳に届きます。図5はフルートとギターの C5 の波形を示していますが、同じ C5 の音を出しても楽器によって波形が大きく異なります。これは、基音に倍音が重なっているためです。
同じ楽器であっても、その作りや材料によって倍音の構成は変わると考えられます。楽器の波形をフーリエ変換すると図6になり、フルートとギターの倍音(C6~E7)の強度がかなり違うことがわかります。実際の波形は不明ですが、手頃な価格のバイオリンと数億円するストラディバリウスでは、波形にかなりの違いが見られるのではないでしょうか。

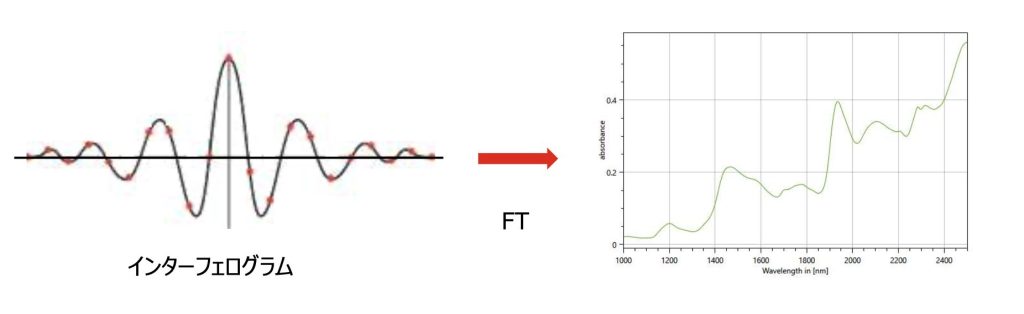
このフーリエ変換は音響分析だけでなく、分析の分野、特にフーリエ変換型赤外分光光度計(FT-IR)やフーリエ変換型近赤外分光光度計(FT-NIR)において中心的な役割を果たしています。FT-IR や FT-NIR の測定で得られるデータは、いろいろな光の成分が合算されたインターフェログラム(干渉パターン)です。
インターフェログラムは、干渉計によって光が干渉し合った結果として得られる、時間軸(または光路差軸)に対する信号の変化ですが、フーリエ変換を使うことで複雑な干渉パターンの中から個々の波数成分を抽出し、物質の構造解析や定量分析が可能になります。図6では横軸データが5個ですが、これが数百から数千のデータが連なる図になります。インターフェログラムの数値データがあれば、Excel の機能を使ってフーリエ変換を行い、スペクトルデータを得ることが可能です。残念ながら現在手元にインターフェログラムの数値データがありません。いずれ試してみたいと思います。













































コメント